データ見て「60%と57%に差あり」と思う人の盲点とは
✍️記事要約
ビジネスにおけるデータの分析や活用がますます重視される中、ビジネスパーソンが身につけておきたい素養の1つが「統計」です。数式を使った複雑な計算をしなければならないと考えがちですが、必ずしもそんなことはありません。また基本的な考え方を知っておくだけでも、冷静な判断がしやすくなります。
そんな「統計」の基礎を身につけるための短期連載第3回は、「データの差」の正しい見方について解説します。
ビジネスでデータを使っていく際に、「その結果に差があるか?」を問われるシーンは意外に多い。
例えば、あるブランドの認知率調査をしたとき、認知率が関東では60%、関西では57%であったとしよう。この結果をみて、あなたはただちに関東のほうが関西よりも認知率が高いと断言できるだろうか。
確かに数字を単純に比べれば、関東のほうが認知率は高い。しかし、“たった3%”の差である。この差は果たして意味のある差なのだろうか。
統計数字を読んでいく時に、あらかじめよく理解しておかなくてはいけないのは、データには偶然の標本誤差が含まれているということである。
■ 「サンプルサイズ」が大きな影響を与える
統計調査では、母集団(調査で性質を明らかにしたい集団)から一部の人(標本)を抽出してデータを集めることが一般的である。こうした調査は「標本調査」と呼ばれる。母集団全員に対して調査しているわけではない以上、標本から得られた調査結果と、母集団全員による真の値との間には差が生じる。これを「標本誤差」と呼ぶ。
標本調査では、標本の選び方によって結果が変わる。特に標本を何人にするかという「サンプルサイズ」は標本誤差の大小に大きな影響を与える。
例えば、母集団が100人だったとき、そこから2人に対して調査を行う場合と、50人に対して調査を行う場合を想像してほしい。100人中2人にしか聞かないのでは、50人に聞いた時に比べて100人全員とのズレが起きやすいこと、すなわち標本誤差が大きいことがイメージできるかと思う。
では、具体的に標本誤差はどのように計算されるのだろうか。実務では、図のような誤差表を使うと便利である。
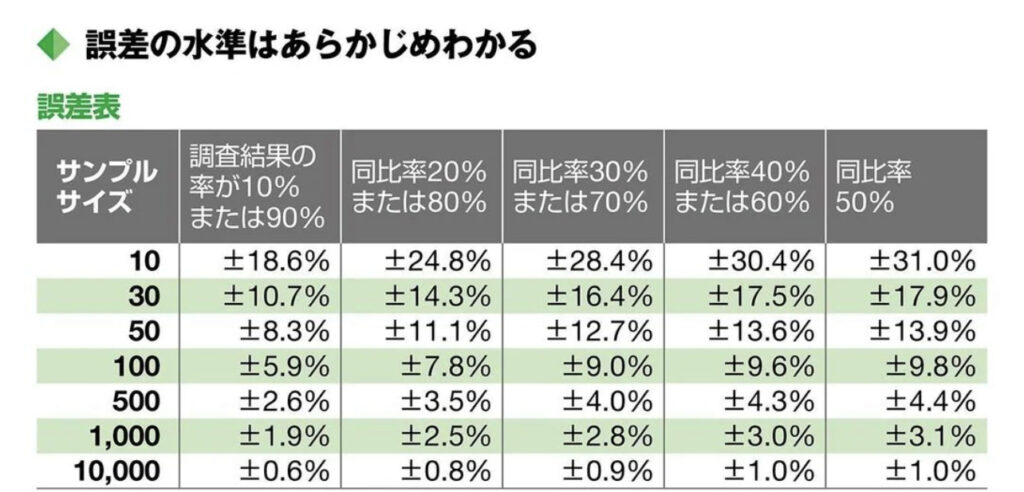
標本誤差は、サンプルサイズと調査結果の比率から計算することが可能である。
例えば、サンプルサイズが1000人で、調査結果の認知率が60%だったとする。このとき、実際に計算をしてみると、標本誤差は±3% (信頼度 95%)になる。すなわち、母集団における真の認知率は、60%の±3%すなわち57%~63%の範囲に収まると、解釈することができるのである。
■ 偶然なのか、意味のある差なのかを判断する方法
このような前提を理解したうえで、冒頭に挙げた2つの調査結果を比較する例を考えてみたい。
関東は60%、関西は57%という結果であったが、それぞれの結果には標本誤差が含まれている。では、私たちはどのようにして、この2つの結果の差を捉えていけばいいのだろうか。こうしたときに役立つのが、「統計的仮説検定」の考え方である。
統計的仮説検定を用いると、先の例で言えば、2つの調査結果の差が、偶然による差なのか、それとも偶然ではなく確かに意味のある差(有意差)なのかを判断することができる。この記事では、統計的仮説検定について具体的に説明していきたい。
ただし、初めて学ぶ人には、統計的仮説検定の考え方は少しなじみにくさがある。理解を深めていくために、まずはそのプロセスを説明したい。
統計的仮説検定は、大きく分けて3つのステップで進められる。
ステップ1は、帰無仮説の設定である。帰無仮説とは、差がない、関係がない等の無(=0)を意味する仮説である。例えば、「関東と関西の認知率に差があるか」を検定するには、「両者の認知率が等しい(差が0である)」という帰無仮説を設定することが必要になる。
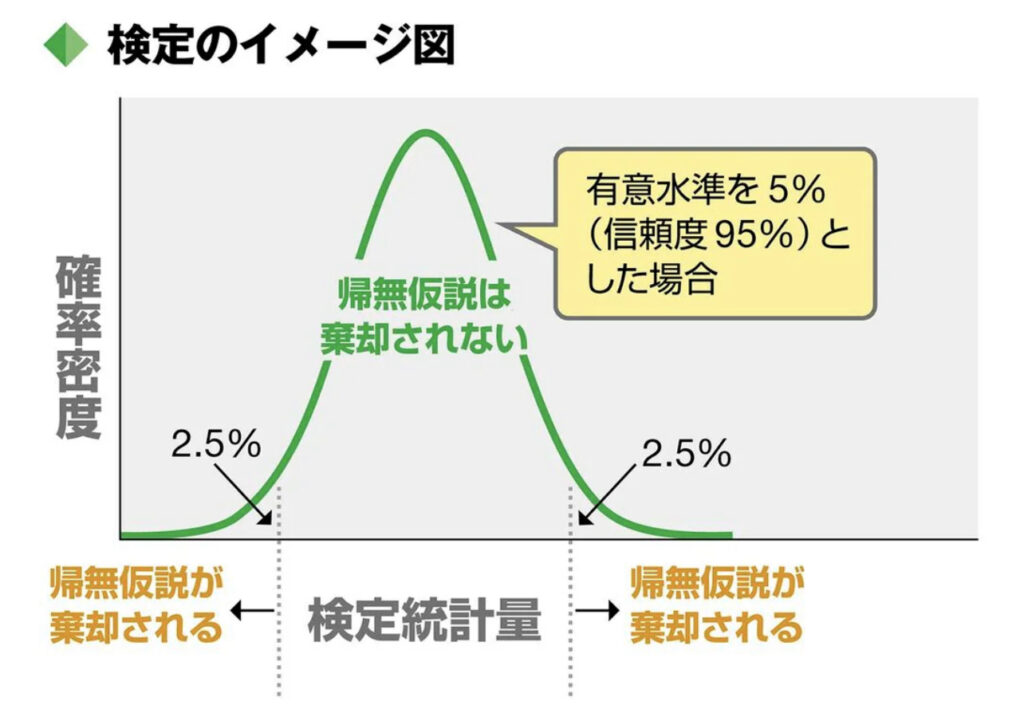
また、分析者はあらかじめ「有意水準」と呼ばれる帰無仮説が間違っていると判断する(棄却する)基準を設定しておく。通常、有意水準には、1%、5%、10%が使われる。5%に設定した場合、100回中5回以下の確率で生じる現象については、めったにおきない非常にまれなことがおきたと判断する基準になる。
ステップ2は検定統計量の計算である。検定統計量は、本記事の例では「両者の認知率が等しいはずなのに実際のデータでは差が出る」事象が“どのくらいまれか”を示す値である。検定統計量にはいくつかの種類があり、用いる検定方法に応じて使い分けられる。
ステップ3は、帰無仮説の棄却である。検定統計量を計算した結果を有意水準と照らす。その結果、めったに起きないことが起きた(偶然にしてはおかしい)のであれば、そもそも帰無仮説が誤りだと棄却し、「関東と関西の認知率には有意差がある」と判断する(対立仮説を採択)。
なぜ統計的仮説検定が初学者になじみにくいかというと、「①帰無仮説を②棄却する」という二重否定のまわりくどい論理を使っているからだ。
関東と関西の認知率には差があるという仮説をもっとシンプルに検証できないのかと思う方もいるかもしれない。しかし、実際には、仮説の正しさを証明するのは難しい。一方、仮説が正しくないことを証明することは反例を1つあげればいいので簡単である。
■ 世の中のすべてのカラスが黒いと証明する方法
この問題を考える時によく挙げられるのが、黒いカラスの例である。今、私たちは「世の中のすべてのカラスが黒いこと」を証明したいとする。
すべてのカラスが黒いことを証明するには、この世のすべてのカラスを観察して黒いことを確かめる必要がある。しかし、すべてのカラスは黒いことが間違っていることを示すには、1匹でも白いカラスを見つければよい。
同様に、本記事の仮説検定の例で言えば、2つの結果に差がないことが間違っていることを示すためには、差がある例を挙げればいい。両者の認知率が等しいはずなのに実際のデータでは差がある、それは偶然にしてはおかしいので、そもそも仮説が正しくないと判断するのである。
こういった考え方は、一般的にはなじみにくいが、科学的な実証においてはよく使われるものなので、ぜひ覚えておきたいものである。
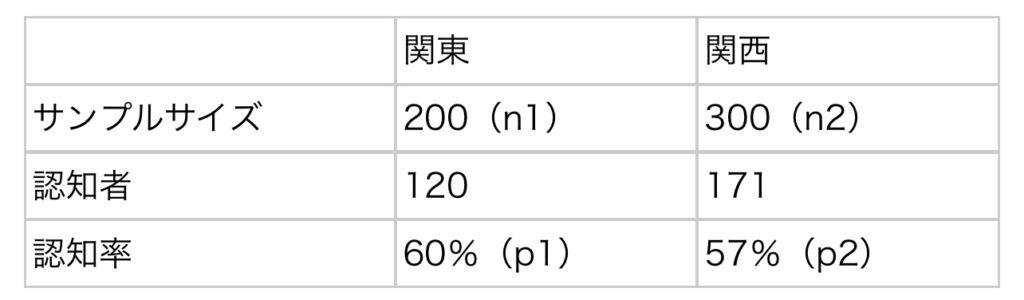
統計的仮説検定の方法を理解していくために、実際の数値に基づいた事例を考えていきたい。ここでは、ビジネスでよく使う、「異なる集団間における比率の差の検定」を例として、実際に検定を行ってみよう。
まず、次のようなデータが得られたとしよう。関東ではサンプルサイズが200人(n1)で認知率が60%(p1)、関西では300人(n2)で57%(p2)であった。ここでは、「関東と関西の認知率に差があるか」を検定したいため、先ほど述べたように「両者の認知率が等しい」という帰無仮説をまず設定する。また、有意水準は5%を設定する。
次に、検定統計量を計算する。異なる集団間における比率の差の検定の場合、検定統計量は、以下のように表すことができる。

式だと難しく感じられる読者の方もいるかもしれないので、実際の数値例も見ていこう。まず、サンプルサイズと認知率のそれぞれの値から加重平均を計算する。ここで、加重平均の分子は認知者の和に等しい。

計算の結果、検定統計量は0.666であった。今回設定した有意水準5%では、1.96以上であれば、有意差ありと判定される。したがって、今回の事例では、帰無仮説は棄却されず、「関東と関西の認知率に(有意な)差があるとはいえない」と結論づけられる。
では、関東では認知率が55%、関西では30%という以下の数表の例ではどうだろうか?
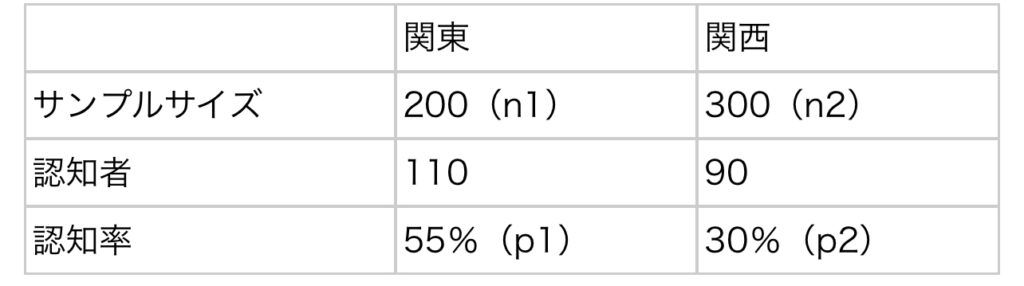
同様に計算すると、検定統計量は5.59であった。これは、有意水準5%のとき検定統計量zの基準である1.96以上であるため、有意差ありと判定される。したがって、この事例では、帰無仮説が棄却され、「関東と関西の認知率に(有意な)差がある」ことを示すことができた。

最後に、検定を行うときに気をつけておきたいポイントを挙げておく。
「有意差がある」というのは「差が大きい」ことを意味しているわけではないことに注意をしておきたい。同じ差でも、サンプルサイズが大きければ有意になり、小さければ有意にならないことがある。仮に10%の差があっても、10人の調査と1000人の調査では、検定の結果は変わる。
したがって、統計的仮説検定は、その結果に「差があることが確からしい」ことを、得られたサンプルサイズの条件下で確認するためのものであることを理解しておきたい。
